量子コンピュータの基本として、1量子ビットの状態についての説明です。
数式が出てきますが、説明も付記し、意味が分かりやすいようにしています。
1量子ビットの視覚的表現として用いられるブロッホ球についての説明を含みます。
量子ビット(qbit)とは?
量子コンピュータの記事を見ていると「ナントカ社がXXX量子ビット数の量子コンピュータを公開!」というような見出しがよくあります。その量子ビットの説明です。
古典コンピュータ(現在、一般に利用されているコンピュータです)で用いられている「ビット」では、1ビットは「0」または「1」の2種類の状態しか表現できません。
「1」の状態のビットを観測すると、(当たり前ながら)「1」になっています。「0」の場合も然りです。
一方、1量子ビットは「0」と「1」の状態が重ねあわされた状態を表現できます。
ある状態の量子ビットを観測した時に状態が確定し、「0」または「1」となります。
(ここで思い出してほしいのが、有名な二重スリット実験です)

えっと、それって逆に使えないんじゃないの?単に、壊れたメモリだよね?

それは違います。量子ビットは状態0と状態1が同時に存在している状態です。量子演算を行うことで、複数の状態を同時に扱うことができます。

なにそれ、すごい!
1量子ビットの数式表現
量子ビットを表現する数式として、1量子ビットの場合は、以下となります。
ここまで、状態0や状態1と表現していた状態は、数式では、|0⟩、|1⟩と表現されます(ディラックさんが考えた表現形式です)
\( | ψ \rangle = α | 0 \rangle + β | 1 \rangle \)
数式の意味としては、以下となります。
状態として |0⟩ と |1⟩ があり、それぞれ確率振幅α、βで重なった状態を |ψ⟩ とする。
ただし、α、βは複素数であり、\( |α|^2 + |β|^2 = 1 \)を満たす。
αとβは「確率振幅」と呼ばれ、複素数の関数です。この絶対値を二乗すると、「確率」になります。つまり、上の数式は、確率\( |α|^2\)で状態0となり、確率\( |β|^2\)で状態1となるとみなせます。

この数式をどのように受け取れば良いんでしょう?

イメージとしては、「状態0、および状態1の確率振幅を示す波α、βがあり、それらから計算できる確率の合計は必ず1になっている」と理解するのが良いと思います。次項のブロッホ球でイメージをつかめます。

ブロッホ球で1量子ビットのイメージが分かるんですね。数式と比べて理解します。
ブロッホ球で表現できるように数式変換する
ブロッホ球で表現できるように、前段で示した以下の数式を変化させていきます。
\( | ψ \rangle = α | 0 \rangle + β | 1 \rangle \tag{1} \)
\( |α|^2 + |β|^2 = 1 \tag{2} \)
確率振幅の式α、βを下記の数式で表現します。
\(α = e^{iφ1}cosθ \tag{3}\)
\(β = e^{iφ2}sinθ \tag{4}\)
式3,4が本当に式2を満たしているのかを確認しましょう。
その前に準備としてオイラーの公式 \( e^{iφ} = cosφ + i sinφ \) を用いて、\(|e^{iφ}| \)の値を求めておきます。
\(|e^{iφ}| = \sqrt{ (cosφ + isinφ)(cosφ – isinφ)} = \sqrt{ (cos^2φ + sin^2φ) } = 1 \)
ということで、任意のφにおいて、\(|e^{iφ}| = 1 \) となることが分かりました。強力な公式です。
準備もできたので、式2を確認しましょう。
\( |α|^2 + |β|^2 = |e^{iφ1}|^2 cos^2θ + |e^{iφ2}|^2 sin^2θ = cos^2θ + sin^2θ = 1 \)
ちゃんと、常に1になります。つまり、式2は常に成立するので、忘れてよいということです。
では、式3,4を式1に代入します。
\( | ψ \rangle = α | 0 \rangle + β | 1 \rangle \)
\(=e^{iφ1}cosθ | 0 \rangle + e^{iφ2}sinθ | 1 \rangle \)
一旦、ここでじっと式を見ます。
さきほど、オイラーの公式で計算した通り、任意のφにおいて、\(|e^{iφ}| = 1 \)となります。
つまり、状態0、1の確率\( |α|^2\)と\( |β|^2\)はパラメータθのみで決定されることが分かります。
では、φ1とφ2は何かというと、これは状態0,1の「確率振幅」の位相を表します。
位相差に意味があるので、位相差のみを残すように式を変換します。
\( | ψ \rangle = e^{iφ1}( cosθ| 0 \rangle + e^{i(φ2-φ1)}sinθ| 1 \rangle ) \)
上の式から、状態0,1への共通係数である\( e^{iφ1} \)はグローバル位相といいます。
状態0,1の相対的な情報だけを残せばよいので、この項は削除します。
また、\(φ=φ2-φ1\)として、式を見やすくします。
\( | ψ \rangle = cosθ| 0 \rangle + e^{iφ}sinθ| 1 \rangle \)
シンプルになりました。
さらに、ブロッホ球で扱いやすいようにθをθ/2に変更します。
\( | ψ \rangle = cos(θ/2)| 0 \rangle + e^{iφ}sin(θ/2)| 1 \rangle \tag{5}\)
\( 0 ≦ θ ≦ \pi \)、\( 0 ≦ φ ≦ 2\pi \)

数式が多くてしんどい・・・。

ブロッホ球を理解するには、最低限として最後の式だけでも見てください。
パラメータとしてθ、φがありますが、状態0,1の確率はθだけで決定し、位相差φは状態0,1の確率に関係しないことが読み取れます。
ブロッホ球での1量子ビットの表現
1量子ビットの状態を視覚的に表現する方法として、地球儀のような「ブロッホ球」が用いられます。
前項の式5と見比べてください。
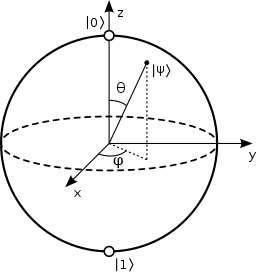
ある1量子ビットの状態は、このブロッホ球の表面のどこかの点として表現されます。
(あくまでも1量子ビットの場合のみの表現手法です。2量子ビット以上の場合は変数が多くなるため、三次元図であるブロッホ球では表現できません)。
ブロッホ球では、北極にあたる部分の状態が「100%の確率で状態0」、逆に南極にあたる部分の状態が「100%の確率で状態1」として表現されます。
前項で記載の通り、状態0,1の確率はθのみで決定されます。状態0,1の位相差φに依存しません。たとえば、ブロッホ球上の赤道の位置にある状態はすべて、状態0,1の確率は、それぞれ0.5と0.5になります。
ブロッホ球を頭にイメージすることで、各種の量子演算を視覚的に理解することができます。例えば、ある量子演算では1量子ビットの状態をブロッホ球の裏側に変化させると理解できます。

1量子ビットの場合のみとはいえ、ブロッホ球は視覚的に理解しやすくて助かります。

各種の量子演算は、ブロッホ球でイメージすると分かりやすいので覚えておくとよいですよ。
まとめ
1量子ビットの数式表現としては、以下となります。
\( | ψ \rangle = α | 0 \rangle + β | 1 \rangle \)
\( |α|^2 + |β|^2 = 1 \)
ブロッホ球の表現に合わせた数式表現としては、以下となります。
\( | ψ \rangle = cos(θ/2)| 0 \rangle + e^{iφ}sin(θ/2)| 1 \rangle \)
\( 0 ≦ θ ≦ \pi \)、\( 0 ≦ φ ≦ 2\pi \)
1量子ビットへの量子演算は、言い換えると、
ブロッホ球の球面上のある点にある1量子ビットを他の点へ移動させる処理
となります。



コメント