量子コンピュータって何？（初心者向け）（３）～ブロッホ球（bloch sphere）上で量子ゲートを操作（three.js）

この記事では、単一量子ビットの量子ゲートの紹介をします。また、ブロッホ球上で量子ゲートを操作できるツールを用意していますので、各量子ゲートがブロッホ球でどのような動きになるかを見ていただきます。

前回のおさらい
単一量子ビットの量子ゲートとブロッホ球の関係
単一量子ビットの量子ゲート
ブロッホ球上での各量子ゲートの動作を見てみよう

前回のおさらい

前回のおさらいです。前記事「量子コンピュータって何？（初心者向け）（２）～１量子ビットとブロッホ球」で示したように単一量子ビットの状態は、ブロッホ球の表面の点で表現できます。

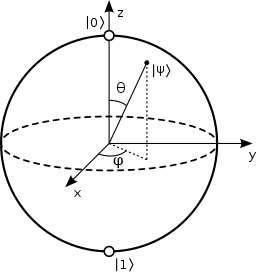
ブロッホ球では、下記の数式で単一量子ビットが表現できます。

\( | ψ \rangle = cos(θ/2)| 0 \rangle + e^{iφ}sin(θ/2)| 1 \rangle \)
\(( 0 ≦ θ ≦ \pi )、( 0 ≦ φ ≦ 2\pi )\)　

単一量子ビットの量子ゲートとブロッホ球の関係

量子ビットは量子ゲートを作用させることで状態を変化させることができます。
ブロッホ球を用いた説明に直すと、「単一量子ビットの状態は量子ゲートを作用させることでブロッホ球面上のある点から、ある点へ移動する」と言い換えることができます。

単一量子ビットの状態は、ブロッホ球の球面上のどこかの点に該当するということですね

そうです。さらに言うと、量子ゲートを作用させることで別の状態に変化させることができます。このページでは単一量子ビット用の主なゲートのみ紹介します。

単一量子ビットの量子ゲート

量子ゲートには色々な種類があります。下表には、単一量子ビットの代表的な量子ゲートを示します。
ブロッホ球上の動きに加えて、数学的計算に用いる行列を示します。

ゲート名	呼称	ブロッホ球上の動き	行列表現
Xゲート	パウリX	X軸を180度回転	\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}
Yゲート	パウリY	Y軸を180度回転	\begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}
Zゲート	パウリZ	Z軸を180度回転	\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}
Hゲート	アダマール変換	X=Z,Y=0の直線を軸に180度回転	\[ \frac{1}{\sqrt2}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\]
Sゲート	位相シフトゲート（90度）	Z軸を90度回転	\begin{bmatrix} 1 & 0 \\ 0 & e^{\frac{i\pi}{2}} \end{bmatrix}
Tゲート	位相シフトゲート（45度）	Z軸を45度回転	\begin{bmatrix} 1 & 0 \\ 0 & e^{\frac{i\pi}{4}} \end{bmatrix}

上表で最初に覚えていただきたい量子ゲートは「Hゲート（アダマール変換）」です。
量子ビットの初期状態｜０＞（ブロッホ球面において、北極点の位置）にHゲート（アダマール変換）を作用させることで、赤道の位置に移動します（下図参照）。これにより、｜０＞と｜１＞の発生確率を50%、50%の状態にすることができます。

数学計算としては、上記のアダマール変換の処理は下記のように示されます。上表の行列と初期状態量子ビット\(\begin{bmatrix}1 \\0\end{bmatrix}\)の掛け算になります。
初期状態量子ビット\(\begin{bmatrix}1 \\0\end{bmatrix}\)は1行目の数値が状態\(| 0 \rangle\)の係数、2行目の数値が\(| 1 \rangle\)の係数を示します。

\( | ψ \rangle = \frac{1}{\sqrt2}\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}
\begin{bmatrix}1 \\0\end{bmatrix}
=\begin{bmatrix}\frac{1}{\sqrt2}\\\frac{1}{\sqrt2}\end{bmatrix}
\)